About Wolfram Cellular Automata

Wolfram cellular automata fill a grid of cells using simple rules to update the state of cells based on neigboring cells. The end result creates larger and more complex patterns from local interactions. Pioneered by Stephen Wolfram, these automata can exhibit diverse behaviors like chaos and showing emergence of order out of chaos. Some rules even have the potential to simulate any computer program.

For more information about Wolfram Cellular Automata, potential applications and implications, see the references page for links to materials.

The goal of this site is to provide a tool that allows individuals to explore different patterns that emerge from wolfram rules and observe behaviors through different initial conditions, edge handling and scales. Since it is the most common way that Wolfram Cellular Automata is demonstrated, this time the visualizer only evaluats top down using the previous row to retrieve the neighborhood used to evaluate a cell state.

Evaluating The Rules

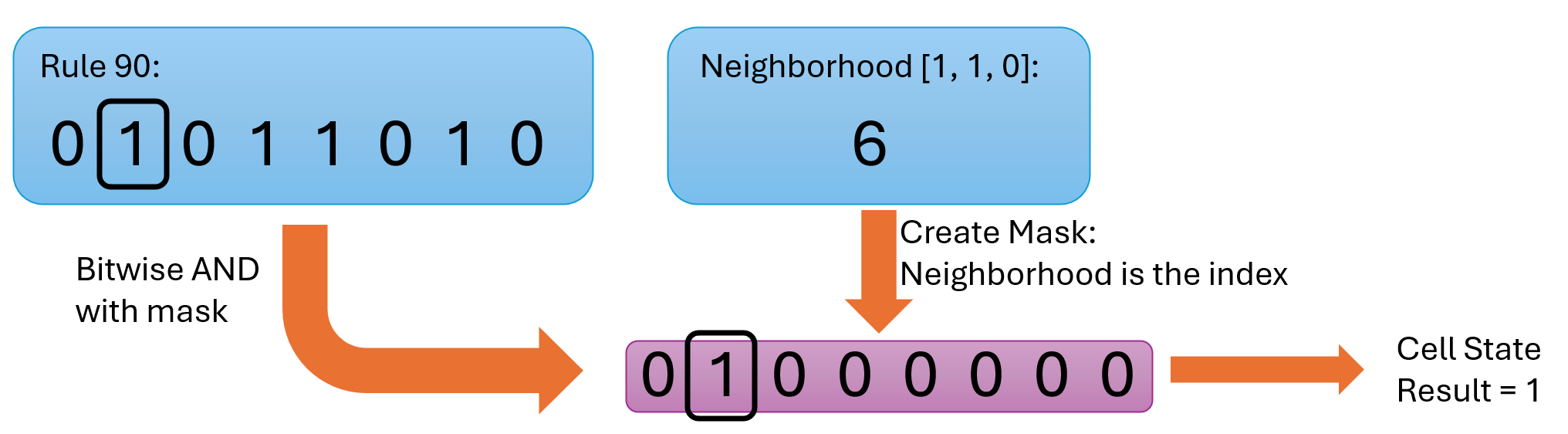
Wolfram rules have a facinating relationship with binary. Most commonly noted is that the rules themselves are derived from the rule number. That is the integer value of a Rule Number when converted to base 2 (binary) is the actual result set for a rules neighborhoods. For example:

While we usually care most about the result, if you look at the neighborhoods it is interesting to note that they are also indexed by binary. That is the integer value of a rule results position when converted to binary is the actual neighborhood for that result. Expanding our example:

This allows for very simple evaluation of a wolfram rule using nothing more than a conversion of base 10 to base 2 along with a bitmask.

                
                    // 1. neighborhood comes in as an array (i.e. [0, 1, 1])

                    // 2. convert the neighborhood into an int value
                    const idx = parseInt(neighborhood.join(''), 2);
    
                    // 3. create a bit mask using the neighborhood number as an index
                    const mask = 1 << idx;
    
                    // 4. return 1 or 0 based on the mask result
                    return (ruleNumber & mask) !== 0 ? 1 : 0;
                
            

Initial States and Boundarys

Some rules can produce a dramatically different result with different inital states and edge handling, while others are relatively stable. The visualizer offers different initial states and edges to choose from, feel free to experiment with these.